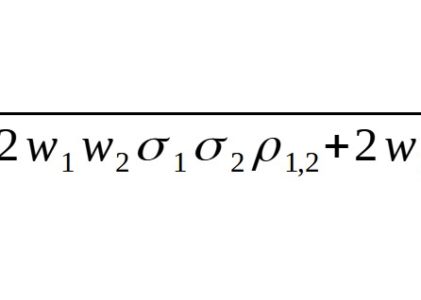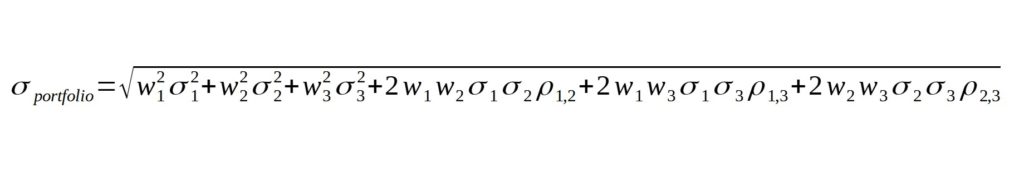A portfolio of 100 stocks can theoretically be less diversified than a portfolio of 20 stocks. By itself, increasing the number of stocks you hold isn’t where the diversification benefits come from. (Though it is related.) The vernacular in finance, specifically stock investing, is to diversify by buying multiple stocks. And so the knee-jerk reaction is to buy as many companies as possible. But believing you’re diversified through owning lots of stocks is a diversification mistake.
Proper diversification is based on correlation. Increasing the number of assets does not inherently reduce risk. While the likelihood of getting low correlation investments increases as the number of assets in a portfolio increases, the diversification benefit is not innately from the number of assets held. Rather, the benefit is based on the correlation among the assets held.
In other words, while owning 100 stocks increases the likelihood of having low correlation assets in the portfolio, the large number isn’t where the diversification benefit comes from. Assuming a 0.60 correlation coefficient among all 100 stocks, you’re likely going to get better diversification benefits from a portfolio of 20 stocks at a 0.20 correlation with each other.
Understanding how correlation affects portfolio risk is key, so we’ll start by having a look at the formula. Then we’ll see how adding perfectly correlated assets affects risk. We’ll also see how adding less than perfectly correlated assets impacts portfolio risk. And finally a discussion on the diminishing benefits of adding more assets. Specifically, why the transaction costs of adding multiple stocks are a compelling reason to start any portfolio with a broad market index fund.
(This is an intermediate-advanced finance topic. For the fundamentals of finance, consider selecting another topic here.)
Page Contents
Portfolio risk formula
The overall risk of a 2-asset portfolio is determined by the following:
- Weights per asset,
- Risks per asset as measured by its returns’ volatility, and
- Correlation coefficient between the two assets.
Formula 1: Two-Asset Portfolio Risk
For a more detailed discussion, see the section Portfolio Risk is NOT the Average Risks of Your Assets.
As you can imagine, the formula for portfolio risk increases in complexity as we add more assets. For a 3-asset portfolio, we’ll need to consider the correlation among all 3 assets. Here’s the formula for our 3-asset portfolio:
Formula 2: Three-Asset Portfolio Risk
Multiplication of matrices, via spreadsheets or similar programs, is necessary for portfolios with a large number of assets.
Adding perfectly correlated assets
We’ll assume there are 2 unique assets to choose from in our hypothetical universe. We then want to build a 2-asset portfolio. In assessing a 2-asset portfolio, our findings should extend to more complex multi-asset portfolios, so we’ll focus on the shorter formula (Formula 1) for simplicity.
The correlation between 2 assets ranges from -1 to 1, with perfectly correlated assets having a correlation coefficient of 1. Substituting 1 to the portfolio risk formula, we end up with basically a weighted average of the risks per asset.
For example, we’ll assume the standard deviations for assets 1 and 2 are 5% and 10%, respectively.
If we made a portfolio holding assets 1 and 2, then portfolio risk is simply the weighted average of 5% and 10%. So if they’re split 50-50, then portfolio risk is 7.5% (50% x 5% + 50% x 10%). If weights are changed to 60-40, then portfolio risk is 7% (i.e., 60% x 5% + 40% x 10%).
Including assets with less than perfect correlation
Adding less than perfectly correlated assets (i.e., a correlation coefficient that’s less than 1) reduces portfolio risk.
Assuming the same standard deviations and weights, we see how a reduction in correlation between the 2 assets reduces the portfolio’s risk. We’ll even assume a relatively high correlation coefficient of 0.90 — this is approximately the correlation between a benchmark like the PSEi and a fund that tracks it like the FMETF.
With a correlation coefficient of 0.90, portfolio risk decreases to 7.33% and 6.83% for a 50-50 split and a 60-40 split, respectively.
At a correlation of 0.20, portfolio risk decreases even more. At 0.20, portfolio risk decreases to 6.02% and 5.46% for a 50-50 split and a 60-40 split, respectively.
In reality, having perfectly correlated assets is highly unlikely, so adding a second asset is expected to reduce risk.
(We haven’t mentioned returns. Our simplifying assumption is that all selected assets have good returns.)
Diminishing benefits
As we add more assets, portfolio risk does decrease, even assuming the same correlation among the 3 assets.
Let’s assume a 3rd asset has a standard deviation of 10%. Assuming the 3rd asset has a correlation of 0.60 with both assets 1 and 2, then a 50-25-25 portfolio of assets 1, 2, and 3, respectively, is estimated to have a portfolio standard deviation of 7.25%. This is a reduction from the 7.33% portfolio risk estimated for the 2-asset portfolio at the same 0.60 correlation.
Notice though that the decrease in risk is marginal.
While adding more and more assets to the portfolio has a diversification benefit, its impact diminishes as we add more assets.
This is how a 20-asset portfolio of low correlation assets can be more diversified than a portfolio of 100 stocks with high correlations. Ray Dalio calls finding 15 to 20 good, uncorrelated, investments the “Holy Grail” of investing. He explains the concept in this video.
Index fund investing
The major takeaway is that while holding multiple assets helps, it is the correlation among these assets that determines the diversification benefit. Owning multiple assets just means you increase your chances of holding assets that have low correlation.
And while the diversification benefits peak at around 15 to 20 uncorrelated assets (at least according to Ray Dalio), it is difficult to know what assets these are. For instance, the stock market is dynamic with changing correlations.
With correlation coefficients that aren’t static, the best way to gain market exposure is through an index fund. The overall transaction costs are lower, and you begin with a fairly diversified portfolio. That is a compelling reason to invest in index funds on a global scale for a truly global portfolio.
(Related: How to Invest in US Stocks from the Philippines (Best Brokers))