Sell more to earn more, right? I mean, why sell 100 units when you can sell 200 units? Does selling more units and do increases in sales mean earning more profit? We instinctively say yes, but it’s not that simple.
Selling more doesn’t always mean more profit. Even in a competitive market, sometimes the right business decision may be to sell less.
And I’m not even talking about price differentiating tactics like when LV bags cost 50 times stock retail brands. Or when business class seats cost a lot more despite providing virtually the same service. Or when scarcity tactics are in play with limited-edition promos.
I’m talking about selling in a competitive market (Wikipedia) where prices are dictated by the public. When is selling less more profitable?
Let’s address the profit maximization problem with an example.
Page Contents
Hypothetical example (selling less to earn more)
Engr. Abad plans to host a course on real estate at a university. He can rent a room with a capacity of 30 students at a rate of 10,000 for the duration of the course. Because the course is on a highly competitive topic and prospective students see other schools as equal alternatives, the price he’s able to sell the course is fixed at 1,000 per student. The course also requires hands-on guidance and he can personally assist only 20 students per session. He will have to hire another colleague at 8,000 if more than 20 students enroll. Handouts and other materials will cost him 300 each.
For simplicity, we will assume these cover all costs. We will also assume that other variable costs are negligible and that there are no other opportunity costs.
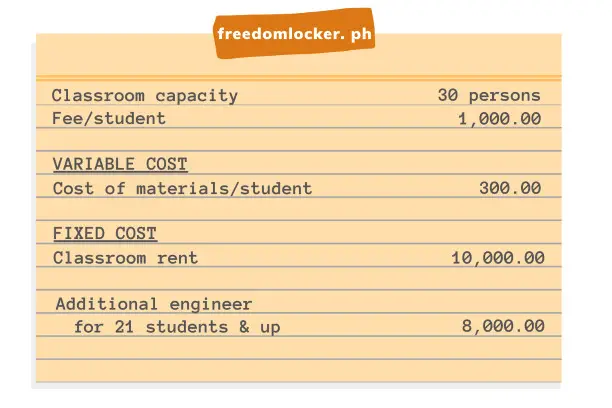
What’s the optimal number of students for his course? (A summarized table of these calculations are found below.)
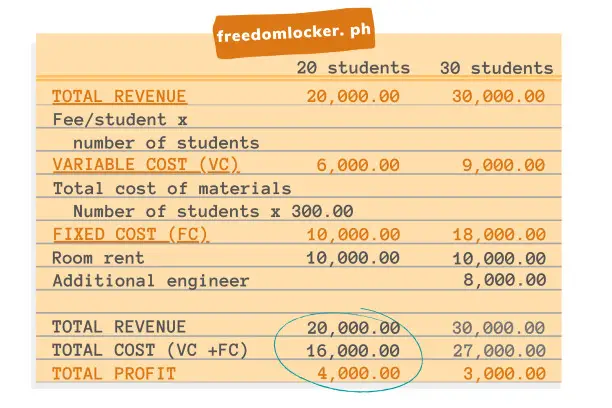
At 20 students, his profit is:
TOTAL REVENUE
Total revenue = 20 students x 1,000 fee per student
Total revenue = 20,000TOTAL COST
Total cost = total fixed costs + total variable costs
Fixed costs
Total fixed costs = rent
Total fixed costs = 10,000
Variable costs
Total variable costs = 20 students x 300 cost per handout and other materials
Total variable costs = 6,000
TOTAL COST
Total cost = total fixed costs + total variable costs
Total cost = 10,000 + 6,000
Total cost = 16,000TOTAL PROFIT
Total profit = total revenue - total cost
Total profit = 20,000 - 16,000
Total profit = 4,000At 30 students, the engineer’s total revenue increases from 20,000 to 30,000 but the need to hire an assistant will also increase costs.
TOTAL REVENUE
Total revenue = 30 students x 1,000 fee per student
Total revenue = 30,000TOTAL COST
Total cost = total fixed costs + total variable costs
Fixed costs
Total fixed costs = rent + 2nd engineer
Total fixed costs = 10,000 + 8,000
Total fixed costs = 18,000
Variable costs
Total variable costs = 30 students x 300 cost per handout and other materials
Total variable costs = 9,000
TOTAL COST
Total cost = total fixed costs + total variable costs
Total cost = 18,000 + 9,000
Total cost = 27,000TOTAL PROFIT
Total profit = total revenue - total cost
Total profit = 30,000 - 27,000
Total profit = 3,000In summary:
Profit decreased from 4,000 (at 20 students) to 3,000 (at 30 students).
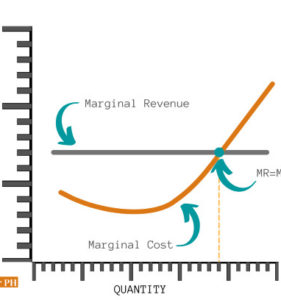
Profit maximization theory
The nonlinear increase in costs isn’t even a farfetched idea. Think of the overtime work that’s needed for more production, or when a piece of equipment reaches capacity. There are a lot of instances when costs don’t increase in a straight line. In other words, doubling production doesn’t automatically double costs — costs can increase by more or by less.
To know at which point profit is maximized, we’ll need to define a few points first.
Marginal revenue (MR)
Marginal revenue is the change in total revenue when you change the number of units sold.
If we change the number of students enrolled from 20 to 21 students, MR is 1,000. In other words, our total revenue changes from 20,000 to 21,000 by changing the number of students from 20 to 21. Our MR from 20 to 21 is therefore 1,000.
In a competitive market, MR is equivalent to our price since we cannot influence what the market is willing to pay for the product or service. In our hypothetical example, our MR is 1,000.
(Note: The market price in a truly competitive market is usually a small amount, closer to insignificance. For example, siomai is in a competitive market while houses are not.)
Marginal cost (MC)
Marginal cost is the change in total cost when you change the number of units sold. At low output levels (e.g., 1 or 2 students enrolled), marginal cost is generally higher versus higher output levels.
This is because costs are spread out over a larger number. If the engineer paid 10,000 as rent while hosting 1 student, that’s essentially paying 10,000 per student. If the same rent of 10,000 is to host 10 students, then the engineer is effectively paying rent at 1,000 per student.
But at some point, costs begin to increase due to several reasons such as capacity limits. See the graph below for a representation of how cost curves look like.
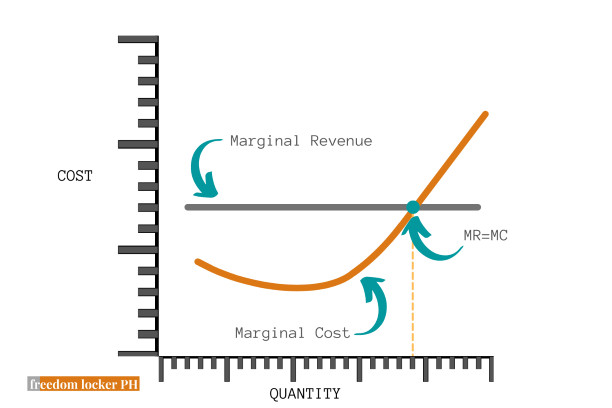
MR = MC (Profit maximization condition)
The profit maximization rule is that as long as your MR is greater than MC, you continue to produce. Let’s unpack this a bit.
MR is what we get from selling one more unit.
MC is what we pay for selling one more unit.
As long as we’re getting more for the next unit sold (i.e., MR > MC), we should continue to produce and sell. In fact, profit is at a maximum when MR = MC. At points over that (i.e., MR < MC), it costs more to acquire the additional sale and profit declines.
Applying what we’ve learned: Focus on profit
We’re all for practical application here at freedom locker PH and I’m not saying we need to compute for MR and MC.
But what I am saying is the decision to produce or sell more isn’t as clear-cut as we might think. And that we need a good understanding of our costs to determine if adding production will yield added profits.
As you’ve seen, increasing production and revenues don’t always increase profit. I picked this topic because it’s a common pitfall a lot of business owners fall into. As business owners, we need a thorough understanding of our fixed costs and variable costs. We need to know how they behave at all levels of production and especially explain how they impact profit.
We’re in business for profit, not revenues.
As business owners, we must turn our focus on profit rather than revenues. Large amounts of revenues can be an ego boost, but it’s not what you ultimately take home. Focus on profit maximization.
(Was this a surprising take or is it common knowledge? Let me know in the comments as it helps me create relevant content.)
Read more, select a topic: