You belong to a special group of people — the group behind my motivations for starting this blog! I’m of the mindset that true financial freedom should be as inclusive as possible. I also know a lot of people shy away from math. And because finance is easily associated with math, the natural reaction is to avoid anything finance. It’s the petty and sad reality, unfortunately. But the notion that finance isn’t for people who hate math is sensationalized. To be fair, finance is one of those subjects that can be as complex or as simple as you want it to be.
But curiously, there are really just a few concepts you need to know for household budgeting and personal finance. We’ll talk about percentages and the time value of money (ignore this phrase for now if it sounds complex), and approach finance from the perspective of people who hate math.
Page Contents
A quick note
Math isn’t difficult, I guarantee. But you do have to have a little bit of mental toughness. This means not giving up at the first sight of a formula, nor hitting the back button when the stress kicks in.
It’s really no different from physical exercise. The first effort is the hardest and it gets easier over time. The effort to try to understand the contents of this post is an investment that’ll pay dividends over your life!
If you absolutely hate math, please consider revisiting this post several times until each section becomes clear. (Bookmark with Ctrl + D on Windows or Cmd + D on a Mac.)
What is a percent?
The etymology of the word “percent” is “per,” as in every, and “cent, ” as in 100. It literally means “for every 100.” Here it is graphically:
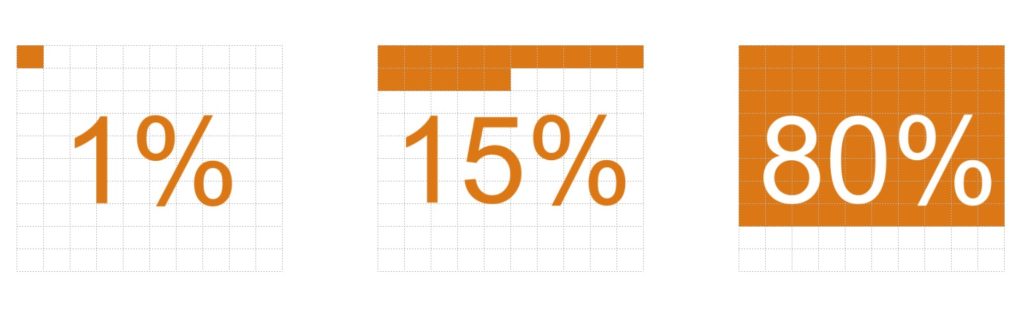
How to compute percentages
Any number can be divided into chunks of 100 pieces and expressed as a percent. I like to think of percentages in decimals: 0.01 to 1.
So “1% to 100%” is really just “0.01 to 1.”
I find it easier because 100% becomes 1, and anything multiplied by 1 is itself. For example, what is 100% of Php3,000? It’s Php3,000 x 1 = Php3,000.
What is 5% of Php2,000? It’s Php2,000 x 0.05, or Php100.
Let’s flip things a bit. Instead of getting the number, let’s try to get the percentage.
To get the percentage of a number, we divide the number in question by the total. For example, Php100 divided by Php2,000 is 0.05, so Php100 is 5% of Php2,000.
Percentages vs. absolute numbers
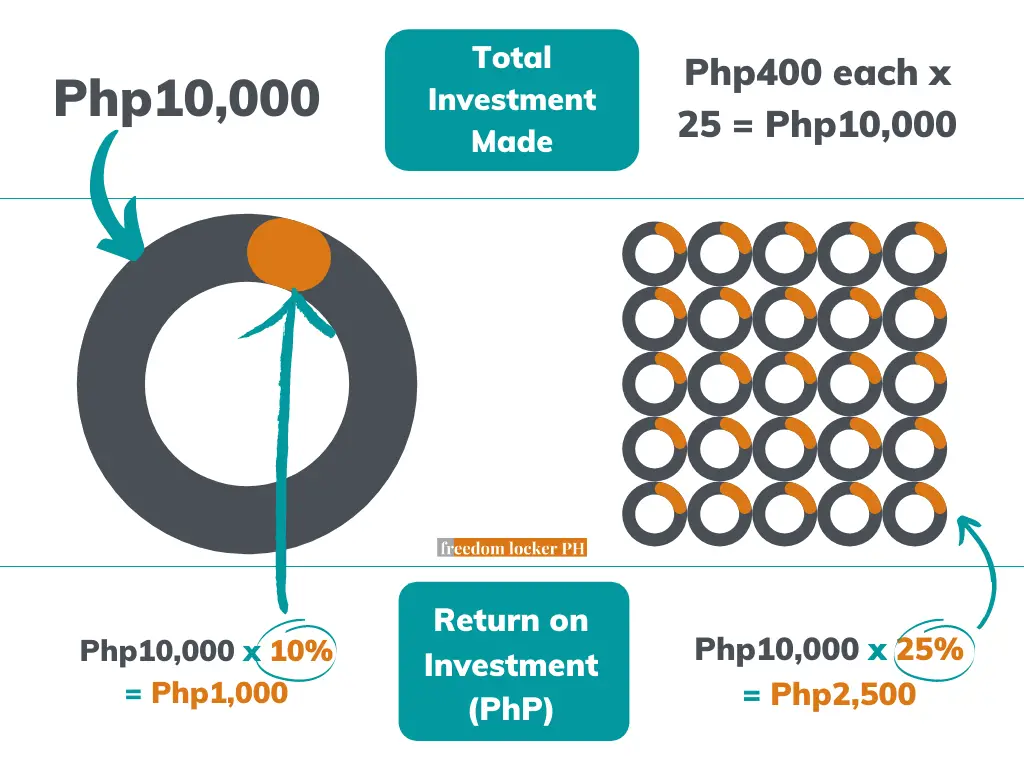
Percentages are helpful when comparing two options because it balances differences in magnitude (size). What does this mean? Say you’re comparing two investments:
- Investment A gives out Php1,000 per year, every year, for 10 years
- Investment B gives out Php100 per year, every year, for 10 years
Judging by these numbers, Investment A seems like the better choice. It is the better choice… UNLESS the costs to acquire these investments are Php10,000 and Php400, respectively. Meaning, to get a hold of Investment A, you’d have to shell out Php10,000. To get Investment B, you’d have to shell out Php400. At these costs, the percentage return per option is:
- Investment A: 1,000 / 10,000 = 0.10 (10%)
- Investment B: 100 / 400 = 0.25 (25%)
In terms of percentages, Investment B is the better choice. So if you had Php10,000 extra money to invest, you’d be better off buying Investment B 25 times (i.e., Php400 each x 25 Investment Bs = Php10,000).
(But computing for ROI is an inferior way of assessing a project. See The unfortunate truth about ROI and payback-period for a slightly more advanced take on project assessment.)
Time value of money

Economics and finance assume humans are rational and selfish. This manifests in our choice to receive Php100 today vs. Php100 one year from now. (Would you rather receive Php100 now or Php100 next year?)
How about one apple 🍎 today vs one apple 🍎 next week? Most would get the apple today.
What if it was one apple 🍎today vs two apples 🍎🍏 next week? It’s not as clear cut as the first example.
This implies the value of Php100 next year isn’t really Php100, but something lower, right? How much lower would you be willing to receive today, and give up the Php100 next year, and feel like it was a fair deal?
Depending on the person, a fair exchange could be Php80, Php90, Php95, or some other number, today vs. Php100 next year. In other words, if I think a fair exchange is at Php80, then the value of Php100 next year (at least for me) is Php80. Meaning:
I could receive Php80 now or Php100 next year and be happy just the same.
The Time Value of Money (TVM) concept in finance explains the difference in value over time. TVM is an application of percentages.
A little mental break before the next section. Fair warning, the subsequent sections contain some formulas. Please do not be intimidated.
Formulas are just sentences expressed in numbers.
Future value (FV), present value (PV), discount rate (r)
In general, the formula is:
FV = PV x (1 + r)The sentence equivalent to this formula is this: “The Future Value of any number is really just its Present Value but multiplied (1 x r)“
Please don’t try to memorize this. A better approach is to understand by dissecting the formula. Let me explain.

In the chicken analogy above, the chicken today (PV) consumes its vitamins (1 + r), and as a result, gets larger (FV). If the vitamins had a negative result, “r” would be negative and the chicken’s future value (FV) would’ve been smaller.
Am I overreaching with the analogy? The point is, the chicken gets larger or smaller depending on what the interest is. Interest is usually positive, so the future value is usually larger (vitamins usually has a positive impact, so the chicken gets fatter tomorrow). Let’s get back to the Php100 example.
Php100 next year or Php80 today?
We already know I’m not willing to accept Php100 next year if I can get Php100 today. But what if it was Php100 next year vs Php80 this year?
If I am willing to accept either Php100 next year (FV) or Php80 today (PV), the difference of Php20 accounts for the gain/loss. Php20 is not the percentage “r,” but is “PV x r.”
(If the 3 succeeding formulas intimidate you, click here to fast forward to what’s important.)
"PV x r" is "80 x 0.25" which is 20In an equation, that is:
FV = PV + (PV x r)Rather than presenting it this way, we say:
FV = PV x (1 + r) ---back to our original formula“(1 + r)” is just saying we’re adding the value of a percentage “r” to PV. So if you want to add 25%, then multiply by (1 + 0.25), or 1.25. If you want to add:
- 10%, then multiply by 1.10
- 50%, then multiply by 1.50
- 75%, then multiply by 1.75
Removing a percentage from any number follows the same steps. If you want to deduct 25%, then multiply by (1 – 0.25), or 0.75. If you want to deduct:
- 10%, then multiply by 0.90
- 50%, then multiply by 0.50
- 75%, then multiply by 0.25
So at a discount rate of 25%, we see that:
FV = PV x (1 + r) OR 100 = 80 x (1 + 0.25) - FV = 100
- PV = 80
- r = 0.25 (25%)
Real examples in the world of finance
After setting aside an emergency fund, excess money is best allocated to where it works hard. What do we mean by working hard? Think of every centavo or penny you have as your employees — every employee should have a role, otherwise, they’re just a waste. Their job is to bring in more money! You can also liken money to soldiers bringing in more soldiers. If you put Php80 in an investment and it generates Php20, your Php80 has just recruited Php20 more soldiers to your army.

Bank deposits
Putting cash in a bank deposit earns you money. Interest rates range from 0% to maybe 0.75%. That is LESS than 1%, not even one box in our first figure above.
In a year’s time, your Php100 would’ve recruited (earned) Php0.75. Php100.75 is still better than Php100, right? Except when you consider (and you should) that the annual inflation in the Philippines in January 2021 was 4.2% and the inflation rate averaged 8.2% from 1958 to 2021 — Trading Economics, Philippines.
If we use the 4.2% (0.042) annual inflation, Php100.75 next year is really just Php96.69 today.
100.75 = PV x (1 + 0.042); divide both sides by (1 + 0.042) to get PV
PV = 100.75 / (1 + 0.042)
PV = 96.69Putting cash in a bank ensures it’s safe and ready-for-use, so it still has merits for sure. But it’s certainly not a place to grow money. Digital banks have softened this toll a bit. They’re theoretically as safe as traditional banks, at least up to the Php500,000 PDIC insured amount, and their lower operating costs allow them to give out higher interest rates — from 2.5% to 4% (as of this writing in February 2021). I talk more about digital banks in Why you NEED a digital bank.
Stock market

They say a buy-and-hold strategy in the stock market yields around 10% p.a. (p.a. means “per annum,” or per year, and is typically what rates are quoted at, unless otherwise specified). A hybrid strategy, based on Warren Buffett’s indicator, that I backtested on the Philippine Stock Exchange (PSE) market could’ve, hypothetically, earned 19% p.a. (How to earn 19% in the stock market, Philippines)
Php100 earning 10% in a year is:
100 x 1.10 = 110So why not invest everything in the stock market? In a word, volatility. The 10% p.a. return is an average, and returns could, for instance, be as high as 20% or as low as negative 20%. Investing Php100 today in the stock market doesn’t guarantee Php110 next year — it’s merely a chance to earn an additional Php10 by next year.
(Volatility is a bit of an intermediate/advanced topic but if you’re interested to know more about it, I touch briefly on what volatility is in this Diversification primer.)
Credit cards
I’m no expert in a lot of things, but especially credit cards. (My wife makes sure they’re paid on time.) But I did check our last statement as part of my research for this post. They charge 2% interest on unpaid balances. Not too bad, until you realize 2% is a MONTHLY RATE. Previously I said rates are typically quoted per annum, for comparability, unless otherwise specified. Apparently, the trend with financial institutions is to give quotations on:
interest paid to us in annual rates but interests paid by us in monthly rates.
Interests quoted in an annual format (i.e., the interests we receive) appear larger and interests quoted in a monthly format (i.e., the interests we pay) appear smaller. It’s likely a strategy tapping into our natural cognitive biases. Daniel Kahneman goes in-depth on this in his book, Thinking, Fast and Slow. Some of my favorite takeaways from the book are in Lessons from Thinking, Fast and Slow.
The 2% monthly interest is in fact 24% interest in a year — well beyond interests received in deposits (0 to 0.75%), from digital banks (2.5% to 4%), or even the average earnings from the stock market. Here’s a graphical comparison between the interest received from bank deposits and interest paid on credit cards:
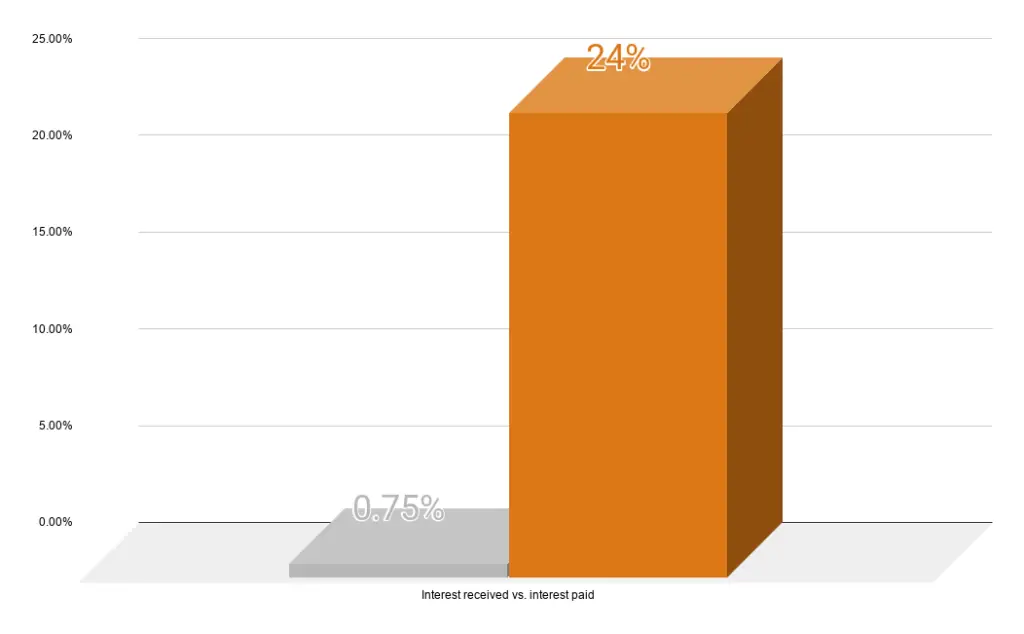
Be wary of credit cards and only use them if you plan on paying the entire balance. Finance charges are unnecessary and avoidable costs.
Businesses
Businesses offer a chance to earn significantly more. But be careful, it’s also merely a chance to earn more, not a guarantee. How much more?
I made this example in Monthly savings will NOT lead to financial freedom. If you use an e-wallet like GCash or PayMaya, you are able to buy Php100 worth of load at Php95. Let’s assume this is what costs retailers to buy the same amount. Retailers sell Php100 worth of load at Php105. That is Php10 earned on a Php95 investment or 10.52%.
10 / 95 = 0.1052 (10.52%)Compounding effect
If you are able to do this consistently, your earned 10.52% could earn their own 10.52%. This is what’s called the compounding effect — interest earned on interest.
Albert Einstein is credited to have said:
Compound interest is the eighth wonder of the world.
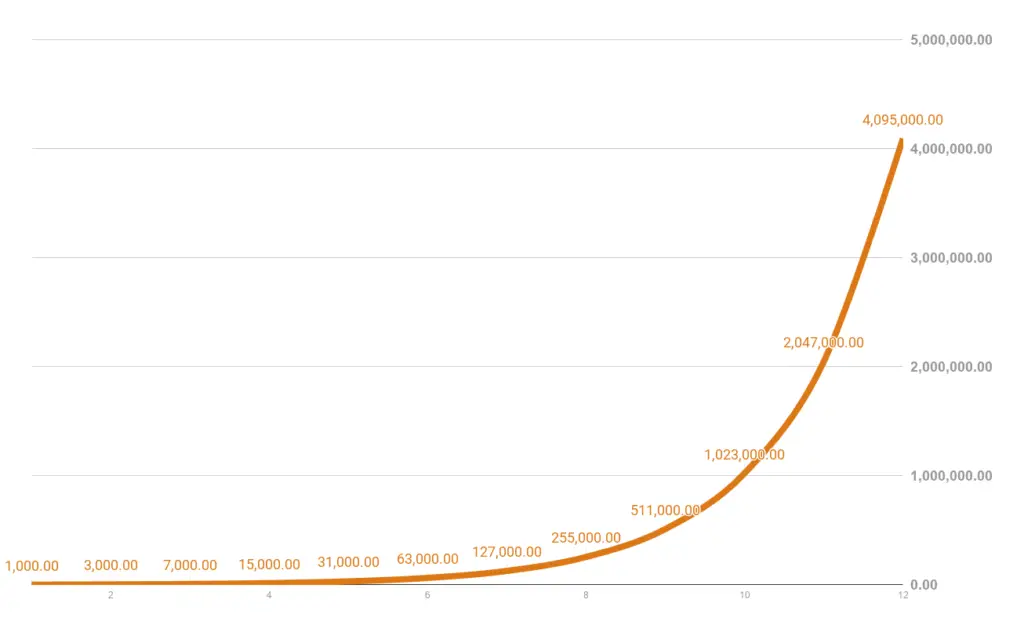
Here’s an example of how powerful compounding can be. Spoiler alert, option 2 is the better choice:
- Option 1: Php1 million next year
- Option 2: 12 monthly payments starting at Php1,000 in Month One but doubled every month (so Php2,000 received in Month Two, and so on)
Doubling is equivalent to earning 100%. Remember, if you want to add 10%, then multiply by 1.10. If you want to add 100%, then multiply by 2 (1 + 1).
Option 2 would’ve given you over Php4 million in one year! Although it takes a long time to catch up (cumulative earnings would’ve been Php1 million by Month Ten), the power of compounding allows Option 2 to yield 4x.
A message for people who hate math
You don’t have to love math to understand personal finance. To be honest, math is mostly about the effort to understand. This is especially true with personal finance where you can get away with knowing just the basics. Malcolm Gladwell touches on this in Chapter 8 of his book Outliers**. Math takes effort to understand, but it’s not complex. When you decide to make an effort, that is also when you understand it. If you can add, subtract, multiply, and divide, you’ve got the foundations covered. Personal finance then becomes a tool, not a burden, towards financial freedom.
*I enjoyed writing this post. Somehow the idea of encouraging someone who hates math to start caring about finance was very gratifying. If you’re the type of person to ask me questions related to this post, I promise to answer your questions! I feel like it’s a low hanging fruit in my hope to encourage more people to strive for financial independence. Do not hesitate to send me a message through our contact form or my Instagram account.
**This is an affiliate link. You may read my affiliate disclosure on my Terms & Conditions page, #6 Links.
Read more, select a topic: